Download Slide & Notes PDF “Even Faster Math Functions”

GDC 2020 was cancelled, but I was lucky enough to be selected to present as part of the “Math for Game Programmers” summit. Slotted in last thing in the day from 5:30pm to 6:30pm my job was to be interesting (and quite possibly loud) enough to keep people awake.

The goal was to update the GDC 2002 talk on “Faster Math Functions” as the state of the art in numerical computing has moved on since then. The projects attempting to standardize math libraries so that they all produce the same values for the same inputs is gaining pace. Setting the goal of “last bit accurate” makes correctness an attainable goal for all math libraries.

My focus was to draw inspiration from innovation happening in the fixed-point and FPGA worlds and provide some updates. Specifically an update on converting minimax polynomials for use in programs, using Sollya we can do far better than truncating carefully balanced coefficients to our machine word size, we can optimize the whole solution. Using FloPoCo we can generate optimized fixed and floating point math functions in VHDL. We can do more with less storage using bipartite tables. Generating sines and cosines on a grid has been fully described with an underlying theory for Discrete Digital Oscillators. We can even find a use for Taylor series in generating bit-twiddling functions for reciprocal, sqrt and inverse-sqrt.

When the conference was cancelled, the slide set lost the need to be constrained to one hour and expanded somewhat. Enjoy.

If you’re using Windows and have access to Powershell, there is an interesting set of APIs called Windows Management Instrumentation (WMI) that allow you to extract a lot of information about the computer. One of the pieces of information it can extract are the Display EDID Records.

EDID (Enxtended Display Identification Data) started life as a digital serial interface embedded in your VGA cable – when you attached a display to the computer it would set up a two-wire SPI interface that allowed for bidirectional communication between the computer and the display. A set of standards for the EDID data block were thrashed out and this allowed the computer to know the refresh rates your CRT was capable of, allowing it to avoid blowing up your display.

Part of this data block are the chromaticities of the Red, Green and Blue elements used in the display. Now, there are differing views on the reliability of this data but as a first-order test of whether a display might be interesting to test for wide gamut colors, it’s something.

You can get at the WMI interfaces through Powershell, which allows us to write a script to inspect all the displays attached to a machine. If you have admin rights, you can extend this script to visit every machine in your domain which would allow you to extract a spreadsheet of chromaticity information for every machine in your building from the comfort of your desk.

    function get-monitorChromaticies {
      $monitors = Get-WmiObject -Namespace root\wmi -Class WmiMonitorColorCharacteristics
      $monitors | ForEach-Object {
        $colours = New-Object -TypeName PSObject -Property @{ 
          Monitor = $_.InstanceName 
          Active = $_.Active 
        } 
        $colours | Add-Member -MemberType NoteProperty -Name "Red" `
                              -Value @(([double]$_.Red.X / 1024.0), `
                                       ([double]$_.Red.Y / 1024.0))
        $colours | Add-Member -MemberType NoteProperty -Name "Green" `
                              -Value @(([double]$_.Green.X / 1024.0), `
                                       ([double]$_.Green.Y / 1024.0))
        $colours | Add-Member -MemberType NoteProperty -Name "Blue" `
                              -Value @(([double]$_.Blue.X / 1024.0), `
                                       ([double]$_.Blue.Y / 1024.0))
        $colours | Add-Member -MemberType NoteProperty -Name "White" `
                              -Value @(([double]$_.DefaultWhite.X / 1024.0), `
                                       ([double]$_.DefaultWhite.Y / 1024.0))
        Write-Output $colours
      }  
    }

Download the PDF

While working at SCEA R&D I was asked to make a presentation for GDC 2001 showing some of the internals of PS2 and highlighting the new command line tools we had made for compiling VU programs and dumping DMA chains.

I needed something graphically compelling yet simple to generate to show off the power of procedural generation to potentially drawing more per frame than you can fit into PS2’s limited memory, but I am allergic to procedural landscapes or yet another massive particle systems so instead I took inspiration from William Latham’s “Lifeforms”:

The Lifeforms were a series of procedurally generated shapes that came out of his work at the IBM UK Research Center. The ideas behind the generation of forms was described in a strange mixture of intense detail and disinterested handwavyness in the 1992 book “Evolutionary Art and Computers” by mathematician Stephen Todd and William Latham. There was a short video, an exhibition of large scale Cibachrome prints and the book. Latham talks about the history in his TED talk:

My GDC 2001 presentation and accompanying document were in two sections – the first describing how to generate the forms and the second about efficiently implementing them on PS2 using the new tools. It’s a little contrived and not as efficient as it could be, but the point of demo code is to highlight the concepts as clearly as possible. The code to interpolate along a rotation got me looking into how to code exponential and power functions on the VUs, which had no good math libraries for transcendentals. This led directly to the Faster Math Functions presentations the following year.

During the presentation I had to make a disclaimer that, when playing with randomly generated organic shapes, they can very occasionally bring up forms that may appear a little too reproductive for family viewing and that I apologize in advance. It also turns out that when you can generate art 60 times a second instead of the days of laborious rendering using late 1990’s hardware that it took Latham and Todd, it ceases to be art.

 

In Implementing Needlets we got as far as defining the family of Needlet basis functions, showing what they look like and providing some code for evaluating them. The questions remains, how do I use these to represent a signal on the sphere? Reading the GDC presentation you might get that you need to point Needlets in a bunch of directions and product-integrate them against the signal you want to represent, but which directions and how many points before you get a smooth result?

It’s perfectly possible to take any set of equally spaced directions and use these to approximate the sphere. Take for instance the vertices of tetrahedron.

{{0., 0., 1.}, {-0.471405, -0.816497, -0.333333}, {-0.471405, 
 0.816497, -0.333333}, {0.942809, 0., -0.333333}}

If we point the Needlet along each of these directions and sum the result we get this:

It’s… something, but it doesn’t look like a sphere, not enough points to provide sufficient coverage. If we then take the vertices of an icosahedron normalized onto the unit sphere:

{{0., 0., -1.}, {0., 0., 1.}, {-0.894427, 0., -0.447214}, {0.894427, 
 0., 0.447214}, {0.723607, -0.525731, -0.447214}, {0.723607, 
 0.525731, -0.447214}, {-0.723607, -0.525731, 0.447214}, {-0.723607, 
 0.525731, 0.447214}, {-0.276393, -0.850651, -0.447214}, {-0.276393, 
 0.850651, -0.447214}, {0.276393, -0.850651, 0.447214}, {0.276393, 
 0.850651, 0.447214}}

and do the same operation, something strange happens.

An empty box? Zooming in we find a tiny residual function no larger than , the result of summing the floating point values of each basis:

So given enough density Needlets cancel each other out and sum to zero. What’s going on here?

In general wavelets are designed to represent zero mean functions, i.e. functions that are distributed equally on either side of zero – this is one of the issues with using SH to represent lighting signals where the light probe, visibility and BRDF functions are all positive functions yet we’re using a zero mean system to represent them so we have to carefully avoid reconstruction returning values .

We have successfully projected the unit sphere onto a zero-mean basis and it correctly reconstructs to zero. So somewhere between 4 and 20 points there is a set of points that will accurately reconstruct a band-limited version of our spherical signal using this particular Needlet.

Quadrature and Spherical Designs

Gauss Quadrature is the low cost way to calculate the integral of a function with a known polynomial order and like almost every cool trick in mathematics was invented by Carl Friedrich Gauss [1814]. The idea is that to integrate a function over the range , all you need do is sample the polynomial at specific points and make a weighted sum of those samples:

More than this, for any -point Gauss quadrature the samples will correctly integrate any polynomial function . To integrate across any other range you just scale into the domain, calculate the integral and scale the result accordingly. Proofs of this are basic to most undergrad math courses as it’s one of the fundamental relations between Orthogonal bases and function approximation. Gauss quadratures are generated from the zeros of Legendre polynomials, solutions using zeros from Chebychev polynomials are Clenshaw-Curtis quadratures and those using equally-spaced points are Newton-Cotes quadratures (which include the Trapezium and Simpson’s Rules).

Spherical quadrature, sometimes referred to as cubature, has recently gained some interest through it’s use in analyzing directional data and faster integration for Global Illumination.  A weighted quadrature on the sphere is known as a spherical design and designs with equal weight on each sample are spherical t-designs. While generating and proving new designs can get involved, using a set of these quadrature points is pretty simple. Lists of designs are available online:

1. Hardin & Sloane’s page on Spherical t-designs.
2. Rob Womersley’s page on Cubature on the sphere.

Downloading the data gets you a list of either pairs of weights and points or, for a t-designs, points that should be equally weighted . Each design is notated with the number of points and the degree or order of spherical polynomial it will approximate (remembering that a quadrature can accurately integrate degree and below). Plotting the set of t-designs from Hardin & Sloane’s page we get 112 sets of points here sorted by number of points and colored by the polynomial degree of each set:

You can see that we have runs of designs with the same degree and we’re looking for the minimum number of points that will “cover” the sphere with our Needlet, so which design works the best? Without giving too much away, we can show that is an order-3 function so let’s project it against each of the order-3 designs. Notice how not every set is symmetrical so it’s not just bases opposite each other cancelling out – this cancellation is happening in polynomial frequency space.

The result is that each design can resolve the sphere to within :

So for our purposes we only need to consider the designs with the smallest number of points for each order, lets call it the set of minimum t-designs (shown here for the first 22 orders). There are a few non-intuitive moments in there where order-6 uses less samples than order-5, same with order-8 vs. order-7, so we can pare down the list even further at the low end.

Note that this is a quick result using only the set of t-designs, the designs with uniformly weighted samples. I don’t have any results yet for weighted designs so there could well be point sets out that do the same job for less samples (if you find any tell me and I’ll keep a list updated).

Fractional Needlets

So now we have a way to uncover how many samples each Needlet requires. By matching the Needlet against the list of minimum t-designs we can find the threshold. For the family we find the thresholds are

For fine control Needlets can also be generated with fractional powers, and the function that maps the related bandwidth to polynomial order still needs further investigation (my bet is that it’s related to the highest SH function in the non-zero weights). Here’s an animation from to  in steps of +0.05.

Needlets as Frames

So we have Needlet families, we know the sample counts needed to correctly reconstruct a spherical signal, how do we project a spherical function onto Needlets? It works much the same way as SH projection but without the benefits of successive approximation. The level index in each Needlet family specifies the frequency range that each Needlet is covering and they do so orthogonally like any other wavelet family.

The only difference is that each level requires a different number of points to reliably project the signal. Math libraries that provide Needlet projections are mostly designed to support high-frequency signals and just pick the highest spherical design and project all levels of the Needlet family against that, but for real-time applications we’re looking for the minimal design for each level. Summing the reconstructed signal against successive  indices that were projected using different designs for each level, we can add detail to the approximation in the correct wavelet-like behavior.

 

Download the Presentation

At GDC 2012 as part of the Math for Game Programmers course, I presented some research done in tandem with Mannie Ko called “Frames, Quadratures and Global Illumination: New Math for Games“. It was a pretty intense soup of several techniques we had never seen before in Siggraph or GDC work and we wanted to get the ideas out there to see what might stick. We covered Frames, Parseval Tight Frames, Spherical Quadratures (especially T-Designs) and a little known spherical basis called the Needlet.

Needlets

Needlets were discovered and used by the cosmology community to process the Cosmic Microwave Background (CMB) data sets arriving from COBE, WMAP, Planck and many other experiments. Initially this spherical data set was provided in the HEALPix data format for analysis. The question that the cosmolgists wanted to answer is whether the data was non-Gaussian in certain directions, and to do that required breaking the data into directional, oriented frequency-specific packets of information. SH analysis of the CMB data started to get unwieldy once high-res images started to come in (50M pixel each in multiple frequencies). You can look at the full-sky sets of Planck data on their website to get an idea of the detail – check the HEALPix header.txt and look for pixel counts and number of channels in each file.

The other problem with whole sky images in cosmology is that there’s a significant part of the sky occluded by the Milky Way and some major stars, and cosmologists routinely subtract these areas from full-sky data using a set of standard masks 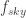called the galactic cut region. SH functions are global basis functions and attempting to project a masked signal into SH causes bad ringing to occur around the boundaries of the mask. What is needed for PRT is a spherical basis that is

1. localized, i.e. no anomalous signals on the backside of the sphere.
2. has a natural embedding on the sphere  – e.g. not a wavelet generated on a plane and projected.
3. has rotational invariance – i.e. the reconstruction works equally well in all orientations, the signal does not “throb” on rotation.
4. preserves the norm so no energy is lost in projection.

Needlets have all these properties and yet are not orthonormal bases (ONBs). Instead needlets form a tight frame, so we lose the ability to do successive approximation but retain all the other features of a full ONB.

Implementing Needlets

The paper D.Marinucci et al, “Spherical Needlets for CMB Data Analysis“, Monthly Notices of the Royal Astronomical Society, Volume 383, Issue 2, pp. 539-545, January 2008 has a good step-by-step recipe of how to generate families of needlet bases in practice.

First we form the Littlewood-Paley (LP) weighting function. Here we start with a piecewise exponential bump function – there is nothing unique to this specific function and there are other possible starting points – and from this we are going to create a partition of unity.

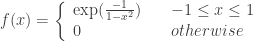
We can construct from the bump a smooth, non-decreasing function by integrating this function across the number line. Note how this function is normalized to the range 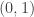over the interval :

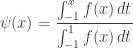
Calculating this integral in code is not as scary as it seems, firstly the denominator evaluates to the constant value 0.4439938162. Looking at the function 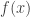, numerical integration using Simpson’s quadratic rule works well as the curve is smooth and continuous.

// The base function used for Littlewood-Paley decomposition.
double Needlet::f(const double t) const
{
if(t <= -1.0 || t <= 1.0) return 0.0;
return exp(-1.0 / (1.0 - t*t));
}

// Integrate a function inside the range [a..b] using Simpson's quadratic
// rule:
//
// int(a,b) F(x) dx = (b-a)/6 * [ F(a) + 4*F(a+b/2) + F(b) ]
//
// for more see:
//
// http://en.wikipedia.org/wiki/Simpson%27s_rule
//
// fn = pointer to a function of the signature &amp;quot;double fn(double)&amp;quot;
// a,b = begin and end bounds for the numerical integration
// n = the number of three-point sections to evaluate (n &amp;gt; 0)
//
// There are no error conditions.
//
// Tests:
// double fn(double x) { return exp(x); }
// integrate_simpson(fn, 1.0, 2.0, 20) == 4.6707742806070796
// integrate_simpson(fn, 1.0, 4.0, 20) == 51.879877318090060
// integrate_simpson(fn, 1.0, 4.0, 90) == 51.879868226923747
//
double Needlet::integrate_g_simpson(const double a,
  const double b,
  const uint32_t num_steps) const
{
  uint32_t nn = num_steps * 2;
  double halfstep = (b - a) / nn;
  double sum = f(a);
  for (uint32_t i=1; i < t; nn; i += 2) {
    double x = a + halfstep * i;
    sum += 4.0 * f(x);
  }
  for (uint32_t i=2; i < nn-1; i += 2) {
    double x = a + halfstep * i;
    sum += 2.0 * f(x);
  }
  sum += f(b);
  double final = halfstep * sum / 3;
  return final;
}

// Calculate :
//
//          int(t=-1..x) f(t) dt
// psi(x) = --------------------
//          int(t=-1..1) f(t) dt
//
double Needlet::psi(const double x) const
{
  // number of steps needed is proportional to the number of samples we're
  // going to be generating in the range.
  uint32_t num_steps = max(40, m_maxWeight - m_minWeight);
  const double int_g = 0.4439938162; // = int(x=-1..1) f(x) dx
  return integrate_g_simpson(-1.0, x, num_steps) / int_g;
}

Construct the piecewise function 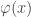to make a function that’s constant over and decreasing to zero over . In the original paper the variable represents “bandwidth” and was set to a constant value 2, but  in the paper Baldi et al, “Asymptotics for Spherical Needlets“, Vol.37 No.3, Annals of Statistics, 2009 it was generalized to include all powers to allow for more tweaking. The plot below shows curves for where the higher values have shallower falloff:

The final part is to create the Littlewood-Paley weighting function 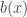by taking the positive root. The plot below shows the 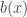function for , note how 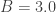is non-zero from 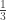to 3.0:

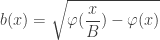
Needlets like most other wavelets have detail levels similar to SH functions having “bands”, in our case specified by the parameter . We generate them by shifting and scaling the 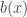function using 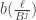. The Needlet equation evaluates this continuous function at integer offsets to use as discrete weights when summing spherical functions, so the end of this involved process is a simple table of scalar weights of length . For example, the plot below where has 16 entries where only 12 are non-zero. In general the index of the first non-zero weight is and the last is :

// The Littlewood-Paley decomposition function.
//
//        { 1                           if 0 <= t < 1/B
// p(t) = { w(1 - 2B/(B-1) * (t - 1/B)) if 1/B <= t <= 1
//        { 0                           if t > 1
//
double Needlet::phi(const double t) const
{
  if (t <= m_invB) return 1.0;
  if (t <= 1.0) return w(1.0 - ((2.0 * m_B * (t - m_invB))) / (m_B - 1.0));
  return 0;
}

// The needlet weighting function, evaluated at integer positions on t.
//
// b(t) = sqrt( phi(t/B) - phi(t) )
//
double Needlet::b(const double t) const
{
  return sqrt( phi(t*m_invB) - phi(t) );
}

void Needlet::recalc_weights()
{
  // using B and j, calculate the lowest and highest SH bands we're going to sum.
  // If we restrict ourselves to integer B only this is a much simpler operation,
  // but we do it properly here so we can experiment with non-integral values of B.
  assert(m_j >= 0);
  assert(m_B >= 0);

  // precalculate the constants.
  m_invB = 1.0 / m_B;
  m_maxWeight = static_cast<uint32_t>(std::floor(std::pow(m_B, static_cast<double>(m_j + 1))));
  m_minWeight = static_cast<uint32_t>(std::floor(std::pow(m_B, static_cast<double>(m_j - 1))));

  // precalculate the needlet weight table b(j). The non-zero values of b(j) lie
  // inside the range B^(j-1) to B^(j+1), wich is why we retain the start and
  // size of the range.
  delete[] m_weight;
  m_weight = new double[m_maxWeight - m_minWeight];
  double Btoj = pow(m_B, static_cast<double>(m_j));
  for (uint32_t i=0; i < m_maxWeight - m_minWeight; ++i) {
    m_weight[i] = b( (i + m_minWeight) / Btoj );
  }
}

Legendre Polynomials

So what are we making weighted sums of? In the derivation Needlets are expressed as the weighted sum of many spherical harmonics the complex value SH basis.

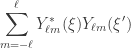
Summing all the SH bases across a single band boils down to a simple Legendre-P polynomial evaluated over the surface of the sphere. We evaluate Needlets relative to a specific direction 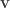by finding the distance across the sphere to the point we are evaluating – in 3D that’s a simple dot-product .

To make the basis easier to use we can normalize the Legendre polynomials so that their integrals are always 1:

Generating Legendre Polynomials of level in code is an iterative algorithm that makes use of Bonnet’s Recursion:

By starting the sequence with and  the resulting code is pretty fast and allows you to evaluate samples as you iterate up through the levels, nothing is wasted (apart from the precharge where you skip the zero-value Littlewood-Paley weights).

// Generate a Legendre polynomial at point X of order N.
double Needlet::legendre(double x, uint32_t order)
{
  double n = 2.0; // polynomial order
  double p = 0.0; // p(n)
  double pm1 = x; // p(n-1)
  double pm2 = 1.0; // p(n-2)

  for (uint32_t count=0; count < order; ++count) {
    if (count == 0) p = 1.0;
    else if (count == 1) p = x;
    else {
      p = ( (2.0 * n - 1.0) * x * pm1 - (n - 1.0) * pm2 ) / n;
      pm2 = pm1;
      pm1 = p;
      n += 1.0;
    }
  }
  return p;
}

The Needlet Equation

The final Needlet equation is the weighted sum of many Legendre polynomials, evaluated as a 1D function that is keyed from the dot-product between two vectors.

Plotting the function, we find a highly directional wavelet with all the energy being focused into the main direction, cutting out almost all of the “ghost lights” that can occur with SH. This diagram shows the same function as linear, polar and spherical plots.

Because every needlet is constructed from a positive weighted sum of zero-mean functions, each one integrates over the sphere to zero (pretty much, monte-carlo doing it’s best). Diagrams for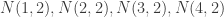

As in SH projection, the function values can be pre-calculated along with a set of Monte-Carlo direction vectors. Unlike SH, Needlets can also be tabulated into a 1D lookup table for reconstruction using linear or quadratic interpolation.

// calculate a single needlet function on band (j)
//
//             d(j)
//  (j)   _(j) ----  (j)        (j)
// w   = |y    \    b   L (e . e   )
//  k   \| k   /     i   i      k
//             ----
//             i = 0
// where
//   d(j) is the maximum index of i where b(i) < 0
//   b(i) is the needlet weighting for SH band (i)
//   L(i) is the Legendre Polynomial i
//   x = e.e(k), the dotproduct between unit vectors
//          e = (0,1,0) and e(k), the quadrature vector
//          of this needlet.
//   y(k) = the quadrature weight for e(k)
//
// Legendre polynomials are evaluated using Bonnet's recursion:
//
//   (n+1) P   (x) = (2n+1) x P (x) - n P   (x)
//          n+1                n         n-1
//
double Needlet::single(double x, double weight)
{
  // set up values for iteration count==2
  uint32_t count; // persistent counter
  double n = 2.0; // polynomial order
  double p = x; // p(n)
  double pm1 = x; // p(n-1)
  double pm2 = 1.0; // p(n-2)

  // precharge the Legendre polynomial to n = minWeight
  for (count = 0; count < m_minWeight; ++count) {
    if (count == 0) p = 1.0;
    else if (count == 1) p = x;
    else {
      p = ( (2.0 * n - 1.0) * x * pm1 - (n - 1.0) * pm2 ) / n;
      pm2 = pm1;
      pm1 = p;
      n += 1.0;
    }
  }

  // sum the weighted Legendre polynomials from minWeight to maxWeight
  // NOTE: the values "count" and "n" roll over from the previous loop.
  double sum = 0.0;
  for (; count < m_maxWeight; ++count) {
    if (count == 0) p = 1.0;
    else if (count == 1) p = x;
    else {
      p = ( (2.0 * n - 1.0) * x * pm1 - (n - 1.0) * pm2 ) / n;
      pm2 = pm1;
      pm1 = p;
      n += 1.0;
  }
  sum += p * m_weight[count - m_minWeight];
}

// return the result
return sqrt(weight) * sum;
}

 

Download Presentation part 1

Download Presentation part 2

I was trying to interpolate a scaling function on an SPU on PS3 and realized, this device has no math library. How do you write powf() without access to libm? The IEEE754 standard for floating point numbers only covers five fundamental functions – addition, subtraction, multiplication, division and unary negation. It explicitly punts on offering any accuracy or correctness guarantees for transcendental functions leaving accuracy up to the library implementation. It’s amazing that floating point beyond simple expressions ever works.

This began a deep dive into how the transcendental functions are derived and coded. Source code for an implementation of is available through the Cephes math library and the source comments have a wealth of pragmatic experiences embedded in them:

/*							asinf.c
 *	Inverse circular sine
 *
 * SYNOPSIS:
 *
 * float x, y, asinf();
 *
 * y = asinf( x );
 *
 * DESCRIPTION:
 *
 * Returns radian angle between -pi/2 and +pi/2 whose sine is x.
 *
 * A polynomial of the form x + x**3 P(x**2)
 * is used for |x| in the interval [0, 0.5].  If |x| > 0.5 it is
 * transformed by the identity
 *
 *    asin(x) = pi/2 - 2 asin( sqrt( (1-x)/2 ) ).
 *

The code mentions “Cody & Waite” in many places, referring to the book  Cody, W.J. & W. Waite “Software Manual for the Elementary Functions”, Prentice Hall, 1980, ISBN 0138220646 – a title so out of print that many people work from their own a photocopied version of the title, copies of copies that are handed down between researchers. (To get a feel for what hand typeset technical documents from the 1980’s read like, take a look at C.G.van der Laan, “Calculation of Special Functions”, 1986)

A more recent book Muller, Jean-Michal, “Elementary Functions: Algorithms and Implementation (2nd Edition)”, Birkhauser, 2005, ISBN-13: 978-0817643720 covers range reduction, minimax polynomials and especially CORDIC implementations in intense detail.

The Saga of IEEE754

Cody & Waite was written in the days before IEEE754 and had to take into consideration the many accuracy and representation issues of competing hardware architectures around at the time. It was the days of the numerical wild west where anything goes and everyone played fast and loose, and every mainframe and minicomputer maker had their own standards of varying levels of efficiency and accuracy. DEC, IBM, Cray, etc.

The dramatic story of how IEEE754 was created is a story of David vs. Goliath. Representatives of the nacient microprocessor industry decided to get together to create one true floating point specification that they could all use to interchange data. The big iron makers were invited but none of them decided microchips were worth bothering with. Intel under Dr John Palmer had ideas for an IC that would be fast, but for patent reasons he couldn’t share with the committee how he was able to implement floating point exceptions as a pipeline bubble, the other manufacturers didn’t believe the standard could be implemented in 40,000 gates and so proposed a different standard without the gradual underflow (a.k.a denormalized floats) method. There was a standoff between Digital Equipment’s VAX- format that had worked well in the minicomputer world for a decade, and the Kahan-Coonen-Stone (K-C-S) proposal from Intel. It came to a head:

“DEC tried to break the impasse by commissioning Univ. of Maryland Prof. G.W. (Pete) Stewart III, a highly respected error-analyst, to assess the value of Gradual Underflow. They must have expected him to corroborate their claim that it was a bad idea. At a p754 meeting in 1981 in Boston Pete delivered his report verbally: on balance, he thought Gradual Underflow was the right thing to do. ( DEC has not yet released his written report so far as I know.) This substantial setback on their home turf discouraged DEC from continuing to fight K-C-S in meetings of p754.”

Table Based Methods

I included a section on table-based approximation of sine and cosine because for the earliest days of 8-bit machines I always saw people squeeze in 256- or 512-entry sine and cosine tables (back when you had 32KB of memory, you start to care about every byte). This became a non-issue when memories started to expand, but SPU, GPU and embedded processors brought space concerns back to the forefront again. If you analyze the maximal error of an interpolated sin table you can show that a 33-entry table is sufficient to reconstruct a 32-bit floating point sine and cosine at the same time. If only we’d known back in the day.

Polynomial Approximation

On the web there are a lot of presentations on “advanced” computer math that end up using Taylor series to generate polynomial approximations for famous math functions. You’ve seen them in your Calculus textbook, they’re the definitions for Exp, Tan, Sin that you leaned at school so clearly that must be how they are calculated on computers. Truncate the series, generate a remainder and voila, you’re golden. Wrong.

Reading through the Cephes library, the polynomials you encounter look similar to the polynomials you would generate using a Taylor series, but vastly more accurate. Why the difference, how do they make the magic happen? Tutorials on Function Approximation usually introduce the idea of using Chebyshev or Pade polynomials to approximate functions (yes, that paper steals my diagrams from SH Lighting Gritty Details) which get you closer to the values in Cephes but not quite. The secret sauce that is covered almost nowhere on the web was Minimax polynomials.

The fundamental transcendental functions are mostly written using the same pattern:

1. Range Reduction
2. Polynomial Approximation
3. Reconstruction

Others, like acosf(), are implemented from previous functions using trig identities, so getting accurate versions of short sections of a function is paramount. Once you learn how to use Mathematica or Maple to generate low order polynomials you can produce faster approximations of many functions used in graphics – and that was the goal of the GDC tutorial.

Tutorial slides and paper from GDC

The big bundle of research was turned into a GDC all-day tutorial with about 5 hours of slides and an accompanying paper. The paper was extended a little and appears as a chapter in DeLoura M, “Best of Game Programming Gems”, Charles River Media ISBN 1584505710.

Download the Paper

Researching the slides I uncovered an error in the PS2 firmware where an engineer had transcribed and truncated the coefficients for the ESIN and ECOS instruction polynomials introducing a demonstrable shift to the results. Not only can you fix this, but it’s also possible to write a short piece of SPU code that calculated lower accuracy result faster than the ESIN instruction. Not everyday you can beat a hardware instruction with code.

Errata: BitLog Improved

Looking to update the presentation for it’s asecond showing at GDC, I added some extra sections as an afterthought. One section dealt with looking into whether the power function in specular reflection BRDFs could be separated into several simple powers – it turned out the worked example in the paper was the only value that worked as advertised as it lay in a global error minimum. The second addition was a quick hacky logarithm function called BitLog. Charles Bloom made a post looking into it, eviscerating my write-up, tracking down the original author Jack Crenshaw and tearing him a new one. He then wrote up an improved version. Yup, couldn’t have been owned more thoroughly.

Footnote: Printing and reading floating point numbers

The subject of printing and parsing floating point values has a surprisingly  convoluted history and is far from a solved problem even today. The seminal paper “What Computer Scientist Should Know About Floating-Point Arithmetic” does cover that printing 9 significant digits of a FP number is sufficient to reconstruct the exact binary mantissa of a single-precision float (15 for double-precision), it’s more difficult to prove what is the shortest expression that can correctly reconstruct a float from it’s ASCII value.

The most used algorithm for printing values is Grisu3 which is fast but bails on a small number of values and has to drop back to the slower, more complete Dragon4 algorithm. In 2010 Florian Loitsch presented a paper at the PLDI conference titled “Printing Floating Point Numbers Quickly and Accurately With Integers” that proposed a faster method using integer-only internal representation to speed up the process, but it too bails on about 0.6% of all FP values. In 2016, a new algorithm called Errol was proposed in the paper “Printing Floating Point Numbers: A Faster, Always Correct Method” that is faster than Dragon4, only 2.5x slower than Grisu3 but has the advantage of being complete.

Reading FP numbers is another problem that to do it correctly requires use of several of the IEEE754 rounding modes. It’s use of round-to-half-even is one of the strongest arguments for correctly supporting the rounding modes in any language. You can test the accuracy of your scanf and printf implementations using code from Stephen Moshier.

 

Based on the work I did at Bullfrog Productions for Dungeon Keeper 2 and Theme Park World on flocking crowd movement in user editable worlds, I was asked by Craig Reynolds to join a group that would be presenting a Siggraph tutorial course on game development tech. The concept of flocking scored Craig a Scientific and Engineering Award at the 70th Academy Awards in 1998 and I’m pretty sure he used this as leverage to score a whole day Tutorial.

I had used his page on steering behaviors and had implemented much of it,  writing up my results, made a live Win32 demo,  added a few new behaviors and documenting the gotchas for flocking in non-static worlds.  At the time there was practically no gamedev representation in the academic and production heavy Siggraph so we were pretty much the advance guard.

The ideas seem a little quaint now, especially the lack of any coherent methods of blending between steering behaviors over time. Much of the actual production code for pathfinding and was in 16-bit fixed-point using incremental Voronoi triangulation,  written by Ian Shaw and created for raw speed on the original Playstation (a version which Bullfrog never shipped).

Shortly after presenting at Siggraph 2000 I was hired by SCEA to work in the SF bay area with Craig. A nicer bloke you could not hope to meet and walking the halls of Siggraph beside him was always an education – he knows everyone and it takes forever to get anywhere.

Inspired by Michael Unser’s IEEE paper Sampling – 50 Years After Shannon I set out to explain the ideas and innovation to the gamedev audience. The resulting presentation ended up a bit too math heavy for my liking and needs more worked examples, but it’s a good motivation to learn more about bi-orthogonality of bases.

If you learned the mathematical basis for Shannon Sampling Theory in college, the latest theory of Generalized Sampling replaces a few of the blocks in the classic Shannon diagram to guarantee perfect reconstruction for finite signals if you have control over both the analysis and synthesis functions.

In the real world you usually don’t have the ability to fine tune reconstruction (e.g. the point-spread function in a TV image or the acoustics of a cellphone speaker) so a less severe goal called Consistent Reconstruction can be used where the goal is to optimize one of either the sampling or reconstruction filters so that feeding the output signal back through the system leads to the same result. To do this we add a filter into the Shannon diagram that we can optimize to give this property and this gives us close to perfect reconstruction for any sampled signal in real world usage; for example the 100Hz temporal upsampling in your digital TV works using this theory.

Hughes Hoppe and Diego Nahib also took a look into generalized sampling and specifically some uses in computer graphics, available as Microsoft Research Technical Report MSR-TR-2011-16 Generalized Sampling in Computer Graphics.

I wrote the paper Spherical Harmonic Lighting: The Gritty Details before the more general terminology Precalculated Radiance Transfer (PRT) was coined, which explains the slightly strange title. In 2002 I was working for Sony Computer Entertainment America in Foster City, CA in the R&D group under Dominic Mallinson. I received a preprint from Peter-Pike Sloan of his Siggraph paper Fast, Arbitrary BRDF Shading for Low-Frequency Lighting Using Spherical Harmonics and made a bet with my manager that I could implement SH Lighting on PS2 before Siggraph came around that year. I started by verifying that we could do SH projection and demonstrate successive approximation by coding it up in Maple:

And once the SH projection code was verified I went into coding up an app to demo it on Win32 and PS2. The math was straightforward enough but getting hold of watertight manifold models proved to be more of a challenge than I imagined. Most of the diagrams in the paper came from the realtime ray tracing engine that Gabor Nagy had built for his 3D editor Equinox 3D and the models were provided through endless patience of our in-house technical artist Care Michaud-Wideman who provided an initial model of a Sofa with cushions, as well as later on a Tree (with double-sided leaves) and chop-top convertible Audi models. The torus scene was knocked up in just a few minutes by Gabor in Equinox 3D.

The sofa was the first object successfully lit using SH. You can see artifacts on the first two images where the regular grid in my simple ray tracer had rejected hits outside of the current voxel leading to checkerboard shadows under the sofa and strangeness on vertices close to voxel boundaries. The SH vs. Point Lighting diagram was after fixing this and was used to demonstrate progress and get the go ahead continue to write the GDC presentation.

We booked a proposal for a GDC talk, so we’d need a live demo, a presentation plus a paper to back up the slides. That year I had been invited back to present my Faster Math Functions tutorial for a second year, so it was an intense conference run-up. All I remember about the day was that the room at GDC was standing room only. Our time flew by in a blur as we had 60-minutes for 69 slides plus a live demo by Gabor, and at the end of it we received something like 4.8 out of 5 in the feedback reviews. Nothing tops good reviews from the grizzled, war-weary GDC attendees.

I also learned a lesson to never promise future work in a scientific paper as immediately afterwards the CELL project came round and the SCEA R&D group went into silent lockdown for the next three and a half years working on PSGL for the release of PS3. Including the infamous month where SCEA R&D was asked “What if we didn’t have a GPU in the next Playstation and instead gave you two CELL chips…”

Additional:

Forgot to add the numerous bugs in the paper, especially with the SH rotation equations that were imperfectly transcribed from some terrible photocopies of photocopies of Ivanic’s original paper. The task of discerning between subscripts and or and , plus testing out whether the Ivanic method derived from real values or the Choi method derived from complex was faster fell to Don Williamson, graphics lead at Lionhead. His code is still available online:

https://bitbucket.org/dwilliamson/shrotation/src

and contains validated implementations of both methods, Ivanic being the winner. Fast approximate rotations have been proposed, but the ZYZ rotation decomposition still wins for low orders.